Conic Sections : Apollonius and Menaechmus Michael Lahanas Απολλώνιος ο Περγαίος, Μέναιχμος ο Θράξ

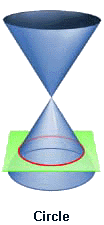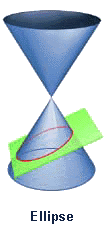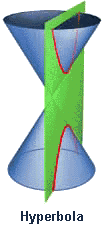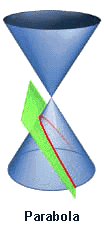
Kegelschnitte: Apollonius und Menaechmus

HYPATIA: Today's subject is conic sections, slices of a cone. A cone — you should be able to remember this — a dunce cap? By passing planes through the cone, various geometric shapes are generated at the intersections. Cut on the horizontal, perpendicular to the axis, we have a circle. Cut at a slight angle, we have an ellipse. Increase the angle a bit more, a parabola.
(Draws on the board) Let us consider the parabola. Where do we find it in nature?
(No response) Come, now. Parse the word. Para — for, bola — throwing. For throwing. What shape is described when you throw a ball into the air? Certainly, a parabola. What shape is described when a furious mob hurls paving stones at the heads of innocent people? Parabolas, all of them... Gerald Everett Jones Hypatia of Alexandria

A conic section (red curve) is the result of an intersection between a cone and a plane. Depending on the angle of intersection, the result can be a hyperbola, parabola, circle, or ellipse.

It is Apollonius of Perga (Απολλώνιος ο Περγαίος ) (about 262 BC - about 190 BC), a Greek geometer, who is usually considered the inventor of the conic sections that leads to the circle, ellipse, parabola and hyperbola that are the possible trajectories of a body in a gravitational field (At least if we ignore some relativistic effects). Apollonius is known as the "Great Geometer" based on his work Conics (Conic secions) , an eight-"book" series on the subject. As he writes ..... I undertook the investigation of this subject at the request of Naucrates the geometer, at the time when he came to Alexandria and stayed with me.. The first four books have come down to us in the original Ancient Greek, but books V-VII are known only from an Arabic translation, while the eighth book has been lost entirely. The Conics is one of the most difficult and complex known mathematical work of ancient Greek mathematicians. Hilal ibn Hilal al-Himsi translated the first four volumes of the Conics while book V to VII were translated by Thabit ibn Qurrah. The Conics is one of the most important mathematical books ever written!

Apollonius wrote many books but only the Conics survived partly. Other books considered that he has written area

1) Cutting-off of an Area
2) Cutting-off of a Ratio
3) Inclinations
4) Plane Loci
5) Quick Delivery (With and unknown method that provides an approximation of 3.1416 for pi )
6) Tangencies

Arabic translation of the Apollonius book V on Conic Sections.

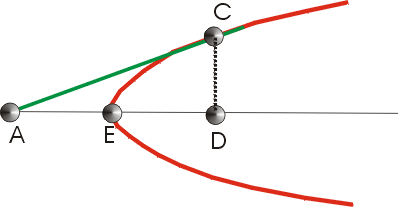
Apollonius used the so-called Symptoms that describes a constant relation between varying magnitudes that depend on the position of an arbitrary point on a curve, example a point C on a parabola. If |AE|= |ED| then AC is a tangent to the parabola

Apollonius showed that only a single normal line can be assigned to each point of a conic section (Coolidge). In the fifth book he discusses evolutes and centers of curvature (Cajori) (or osculation as mentioned by Euler in Introductio in analysin infinitorum 1748 ). Apollonius therefore was of the first who considered the curvature and elements of differential geometry.

Menaechmus (Μέναιχμος ) (from Alopeconnesus or Proconnesus) earlier (about 380 BC- about 320 BC) showed that circle, ellipses, parabolas, and hyperbolas are obtained by cutting a cone with a plane. He was born in Alopeconnesus, (now Turkey) and was a student of Plato and , one can observe the "upward curvature" of the stylobate (the platform on which the columns rest). In fact, there are no straight lines anywhere in the Parthenon. Everything is slightly curved. In particular, the deep foundation, the stylobate, and the entablature is higher in the center (ca. 2 1/2 inches on the short sides and ca. 4 1/2 inches on the flanks) than it is an the corners. This upward curvature is found in some other Doric temples, but the Parthenon is the most exaggerated and perfect example. The curve appears to be parabolic (a regular conic section). . According to