|
|
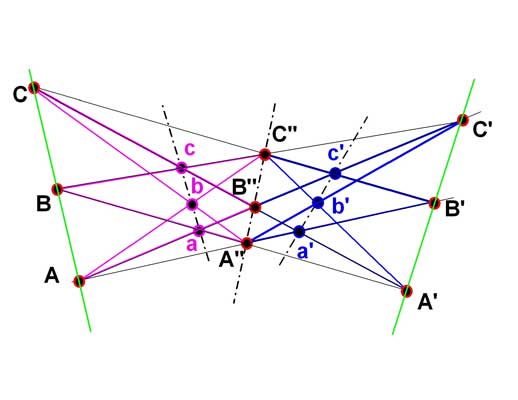
Griechische Mathematik: Pappos von Alexandria Bees were endowed with a certain geometrical forethought .... There being, then, three figures which of themselves can fill up the space round a point, viz. the triangle, the square and the hexagon, the bees have wisely selected for their structure that which contains the most angles, suspecting indeed that it could hold more honey than either of the other two. Pappus of Aelxandria Pappus (or Pappos) of Pappus's Hexagonal Theorem If ABC and A'B'C' are straigth lines; and A'', B'', C'' are the intersections of AB' with A'B, AC' with A'C, BC' with B'C respectively: then A''B''C'' is a straight line.
What Pappus did not know is what happens if we continue the process with the new line A''B''C'' and the original lines ABC and A'B'C' :
In a new iteration we obtain two new lines abc and a'b'c' and we can continue this process further. An example from an article written by Marcel Berger is shown after 5 iterations. If the process continues the result is a fractal structure with interesting mathematical properties. See: Richard Evan Schwartz, Pappus's theorem and the modular group. Publications Mathématiques de l'IHÉS, 78 (1993), p. 187-206 ()
Marcel Berger, Das Unendliche in der Geometrie (The Infinite in Geometry), Spektrum Spezial: Das Unendliche, p. 38, ND 1/2003.
|