Johannes Kepler

Johannes Kepler (December 27, 1571 – November 15, 1630), a key figure in the scientific revolution, was a German mathematician, astronomer, astrologer, and an early writer of science fiction stories. He is best known for his laws of planetary motion, based on his works Astronomia nova, Harmonice Mundi and the textbook Epitome of Copernican Astronomy.

Through his career Kepler was a mathematics teacher at a Graz seminary school (later the University of Graz), an assistant to Tycho Brahe, court mathematician to Emperor Rudolf II, mathematics teacher in Linz, and court astrologer to General Wallenstein. He also did fundamental work in the field of optics and helped to legitimize the telescopic discoveries of his contemporary Galileo Galilei.

He is sometimes referred to as "the first theoretical astrophysicist", although Carl Sagan also referred to him as the last scientific astrologer.

Portrait of Kepler by an unknown artist, 1610

Life

Childhood and education (1571–1594)

Kepler was born on December 27, 1571 at the Imperial Free City of Weil der Stadt (now part of the Stuttgart Region in the German state of Baden-Württemberg, 30 km west of Stuttgart's center). His grandfather had been Lord Mayor of that town, but by the time Johannes was born, the Kepler family fortunes were in decline. His father earned a precarious living as a mercenary, and he left the family when Johannes was five years old. He was believed to have died in the war in the Netherlands. His mother, an inn-keeper's daughter, was a healer and herbalist who was later tried for witchcraft. Born prematurely, Johannes claimed to have been a weak and sickly child. Despite his ill health, he was precociously brilliant. As a child, he often impressed travelers at his grandfather's inn with his phenomenal mathematical faculty.

He was introduced to astronomy/astrology at an early age, and he developed a love for it that would span his entire life. At age five, he observed the Comet of 1577, writing that he "was taken by [his] mother to a high place to look at it." At age nine, he observed another astronomical event, the Lunar eclipse of 1580, recording that he remembered being "called outdoors" to see it and that the moon "appeared quite red". However, childhood smallpox left him with weak vision, limiting him to the mathematical rather than observational aspects of astronomy.

In 1589, after moving through grammar school, Latin school, and lower and higher seminary in the Lutheran education system, Kepler began attending the University of Tübingen as a theology student, where he proved himself to be a superb mathematician and earned a reputation as a skillful astrologer. Under the instruction of Michael Maestlin, he learned both the Ptolemaic system and the Copernican system; he became a Copernican at that time, defending heliocentrism from both a theoretical and theological perspective in student debates. Despite his desire to become a minister, near the end of his studies, Kepler was recommended for a position as teacher of mathematics and astronomy at the Protestant school in Graz, Austria. He accepted the position in April 1594, at the age of 23.

Early career (1594–1601)

In Graz, Kepler began developing an original theory of cosmology based on the Copernican system, which was published in 1596 as Mysterium Cosmographicum—The Sacred Mystery of the Cosmos.

In April 1597, Kepler married Barbara Müller. She died in 1611 and was outlived by two of Johannes's children and one by an earlier marriage.

In December 1599, Tycho Brahe wrote to Kepler, inviting Kepler to assist him at Benátky nad Jizerou outside Prague. Pressured to leave Graz by increasingly strict Counter-Reformation policies restricting the religious practices and political rights of Protestants, Kepler joined Tycho in 1600. After Tycho's death in 1601, Kepler was appointed Imperial Mathematician in his place, a post he would retain through the reigns of three Habsburg Emperors (from November 1601 to 1630).

Imperial Mathematician in Prague (1601–1612)

As Imperial Mathematician, Kepler inherited Tycho's responsibility for the Emperor's horoscopes as well as the commission to produce the Rudolphine Tables. Working with Tycho's extensive collection of highly accurate observational data, Kepler also set out to refine his earlier theories but was forced to abandon them. Instead, he began developing the first astronomical system to use non-circular orbits; it was completed in 1606 and published in 1609 as Astronomia Nova—New Astronomy. Astronomia Nova contained what would become the first and second laws of planetary motion.

In October 1604, Kepler observed the supernova which was subsequently named Kepler's Star (a term which may also refer to the stellated octahedron). In 1611, Kepler published (as a letter to a friend) a monograph on the origins of snowflakes, the first known work on the subject. He correctly theorized that their hexagonal nature was due to cold, but did not ascertain a physical cause for this. In January 1612, the Emperor died. To escape the growing religious tension in Prague, Kepler took the post of Provincial Mathematician in Linz.

Teaching in Linz and final years (1612–1630)

In 1615, Kepler married Susanna Ruettinger, with whom he would have several children.

In 1617, Kepler's mother Katharina was accused of being a witch in Leonberg. Beginning in August 1620 she was imprisoned for fourteen months. Thanks in part to the extensive legal defense drawn up by Kepler, she was released in October 1621 after failed attempts to convict her. However, she was subjected to territio verbalis, a graphic description of the torture awaiting her as a witch, in a final attempt to make her confess. Throughout the trial, Kepler postponed his other work (on the Rudolphine Tables and a multi-volume astronomy textbook) to focus on his "harmonic theory". The result, published in 1619 as Harmonices Mundi ("Harmony of the Worlds") contained the third law of planetary motion.

Kepler completed the last of seven volumes of his textbook Epitome of Copernican Astronomy in 1621, which brought together and extended his previous work and would become very influential in the acceptance of the Copernican system over the next century. In 1627 he completed the Rudolphine Tables, which provided accurately calculated future positions of the planets and allowed the prediction of rare astronomical events.

On November 15, 1630 Kepler died of a fever in Regensburg. In 1632, only two years after his death, his grave was demolished by the Swedish army in the Thirty Years' War.

Work

Kepler lived in an era when there was no clear distinction between astronomy and astrology, while there was a strong division between astronomy/astrology (a branch of mathematics within the liberal arts) and physics (a branch of the more prestigious discipline of philosophy). He also incorporated religious arguments and reasoning into his work, such that the basis for many of his most important contributions was essentially theological (Barker & Goldstein, 2001).

Kepler was a Pythagorean mystic. He considered mathematical relationships to be at the base of all nature, and all creation to be an integrated whole. This was in contrast to the Platonic and Aristotelian notion that the Earth was fundamentally different from the rest of the universe, being composed of different substances and with different natural laws applying. In his attempt to discover universal laws, Kepler applied terrestrial physics to celestial bodies; famously, his effort produced the three Laws of Planetary Motion. Kepler was also convinced that celestial bodies influence terrestrial events. One result of this belief was his correct assessment of the moon's role in generating the tides, years before Galileo's incorrect formulation. Another was his belief that someday it would be possible to develop a "scientific astrology", despite his general disdain for most of the astrology of his time.

Scientific work

Kepler's laws

Kepler inherited from Tycho Brahe a wealth of the most accurate raw data ever collected on the positions of the planets. The difficulty was to make sense of it. The orbital motions of the other planets are viewed from the vantage point of the Earth, which is itself orbiting the sun. As shown in the example below, this can cause the other planets to appear to move in strange loops. Kepler concentrated on trying to understand the orbit of Mars, but he had to know the orbit of the Earth accurately first. In order to do this, he needed a surveyor's baseline. In a stroke of pure genius, he used Mars and the Sun as his baseline, since without knowing the actual orbit of Mars, he knew that it would be in the same place in its orbit at times separated by its orbital period. Thus the orbital positions of the Earth could be computed, and from them the orbit of Mars. He was able to deduce his planetary laws without knowing the exact distances of the planets from the sun, since his geometrical analysis needed only the ratios of their solar distances.

Unlike Brahe, Kepler held to the heliocentric model of the solar system. Starting from that framework, Kepler made twenty years of painstaking trial-and-error attempts at making some sense out of the data. He finally arrived at his three laws of planetary motion:

Using these laws, he was the first astronomer to successfully predict a transit of Venus (for the year 1631). Kepler's laws were the first clear evidence in favor of the heliocentric model of the solar system, because they only came out to be so simple under the heliocentric assumption. Kepler, however, never discovered the deeper reasons for the laws, despite many years of what would now be considered non-scientific mystical speculation. Isaac Newton eventually showed that the laws were a consequence of his laws of motion and law of universal gravitation. (From the modern vantage point, the equal-area law is more easily understood as arising from conservation of angular momentum.)

Kepler first discovered his distance-cubed-over-time-squared (or 'third') law of planetary motion on March 8, 1618 but rejected the idea until May 15, 1618, when he verified his result. This result was published in his Harmonices Mundi (1619).

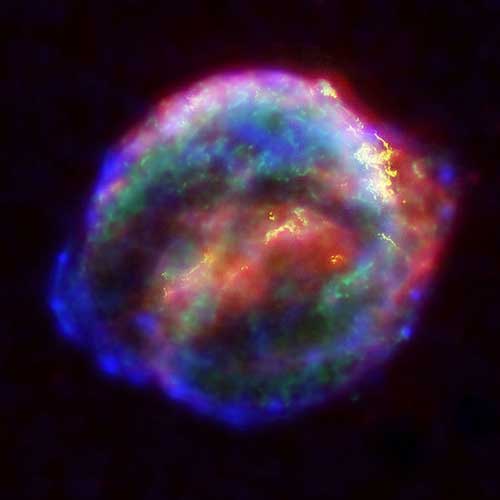
Supernova 1604

On October 17, 1604, Kepler observed that an exceptionally bright star had suddenly appeared in the constellation Ophiuchus. (It was first observed by several others on October 9.) The appearance of the star, which Kepler described in his book De Stella nova in pede Serpentarii ("On the New Star in Ophiuchus's Foot"), provided further evidence that the cosmos were not changeless; this was to influence Galileo Galileo in his argument. It has since been determined that the star was a supernova, the second in a generation, later called Kepler's Star or Supernova 1604. No further supernovae have been observed in the Milky Way, though others outside our galaxy have been seen.

Remnant of Kepler's Supernova SN 1604 (NASA)

Other scientific and mathematical work

Kepler also made fundamental investigations into combinatorics, geometrical optimization, and natural phenomena such as snowflakes, always with an emphasis on form and design. He was also one of the founders of modern optics, defining for example antiprisms and the Kepler telescope (see Kepler's books Astronomiae Pars Optica—i.a. theoretical explanation of the camera obscura—and Dioptrice). In addition, since he was the first to recognize the non-convex regular solids (such as the stellated dodecahedra), they are named Kepler solids in his honor.

Kepler also was in contact with Wilhelm Schickard, inventor of the first automatic calculator, whose letters to Kepler show how to use the machine for calculating astronomical tables.

Mysticism and astrology

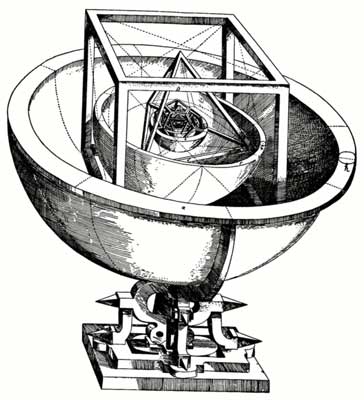
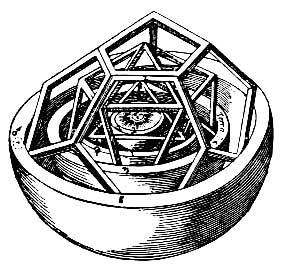
Kepler's Platonic solid model of the Solar system from Mysterium Cosmographicum (1596), Closeup of inner section of the model

Mysticism

Kepler discovered the laws of planetary motion while trying to achieve the Pythagorean purpose of finding the harmony of the celestial spheres. In his cosmologic vision, it was not a coincidence that the number of perfect polyhedra was one less than the number of known planets. Having embraced the Copernican system, he set out to prove that the distances from the planets to the sun were given by spheres inside perfect polyhedra, all of which were nested inside each other. The smallest orbit, that of Mercury, was the innermost sphere. He thereby identified the five Platonic solids with the five intervals between the six known planets (Mercury, Venus, Earth, Mars, Jupiter, Saturn) and the five classical elements.

Kepler's Platonic solid model of the Solar System, from Mysterium Cosmographicum (1596)

In 1596 Kepler published Mysterium Cosmographicum, or The Sacred Mystery of the Cosmos. Here is a selection explaining the relation between the planets and the Platonic solids:

Before the universe was created, there were no numbers except the Trinity, which is God himself… For, the line and the plane imply no numbers: here infinitude itself reigns. Let us consider, therefore, the solids. We must first eliminate the irregular solids, because we are only concerned with orderly creation. There remain six bodies, the sphere and the five regular polyhedra. To the sphere corresponds the heaven. On the other hand, the dynamic world is represented by the flat-faces solids. Of these there are five: when viewed as boundaries, however, these five determine six distinct things: hence the six planets that revolve about the sun. This is also the reason why there are but six planets…

Close-up of an inner section of Kepler's model

I have further shown that the regular solids fall into two groups: three in one, and two in the other. To the larger group belongs, first of all, the Cube, then the Pyramid, and finally the Dodecahedron. To the second group belongs, first, the Octahedron, and second, the Icosahedron. That is why the most important portion of the universe, the Earth—where God's image is reflected in man—separates the two groups. For, as I have proved next, the solids of the first group must lie beyond the earth's orbit, and those of the second group within… Thus I was led to assign the Cube to Saturn, the Tetrahedron to Jupiter, the Dodecahedron to Mars, the Icosahedron to Venus, and the Octahedron to Mercury…

To emphasize his theory, Kepler envisaged an impressive model of the universe which shows a cube, inside a sphere, with a tetrahedron inscribed in it; another sphere inside it with a dodecahedron inscribed; a sphere with an icosahedron inscribed inside; and finally a sphere with an octahedron inscribed. Each of these celestial spheres had a planet embedded within them, and thus defined the planet's orbit.

In his 1619 book, Harmonice Mundi or Harmony of the Worlds, as well as the aforementioned Mysterium Cosmographicum, he also made an association between the Platonic solids with the classical conception of the elements: the tetrahedron was the form of fire, the octahedron was that of air, the cube was earth, the icosahedron was water, and the dodecahedron was the cosmos as a whole or ether. There is some evidence this association was of ancient origin, as Plato tells of one Timaeus of Locri who thought of the Universe as being enveloped by a gigantic dodecahedron while the other four solids represent the "elements" of fire, air, earth, and water. To his disappointment, Kepler's attempts to fix the orbits of the planets within a set of polyhedrons never worked out, but it is a testimony to his integrity as a scientist that when the evidence mounted against the cherished theory he worked so hard to prove, he abandoned it.

His most significant achievements came from the realization that the planets moved in elliptical, not circular, orbits. This realization was a direct consequence of his failed attempt to fit the planetary orbits within polyhedra. Kepler's willingness to abandon his most cherished theory in the face of precise observational evidence also indicates that he had a very modern attitude to scientific research. Kepler also made great steps in trying to describe the motion of the planets by appealing to a force which resembled magnetism, which he believed emanated from the sun. Although he did not discover gravity, he seems to have attempted to invoke the first empirical example of a universal law to explain the behaviour of both earthly and heavenly bodies.

Astrology

Kepler disdained astrologers who pandered to the tastes of the common man without knowledge of the abstract and general rules, but he saw compiling prognostications as a justified means of supplementing his meager income. Yet, it would be a mistake to take Kepler's astrological interests as merely pecuniary. As one historian, John North, put it, "had he not been an astrologer he would very probably have failed to produce his planetary astronomy in the form we have it." However, Kepler's views on astrology were quite unconventional for his time; he argued for a system of astrology based largely on harmonics, a type of 'planetary harmonics' based almost entirely upon the astrological aspects and what has been traditionally been termed "the music of the spheres." Information relating to his theories can be found in his book Harmonice Mundi.

Kepler believed in astrology in the sense that he was convinced that astrological aspects physically and really affected humans as well as the weather on Earth. He strove to unravel how and why that was the case and tried to put astrology on a surer footing, which resulted in the On the more certain foundations of astrology (1601), in which, among other technical innovations, he was the first to propose the quincunx aspect. In The Intervening Third Man, or a warning to theologians, physicians and philosophers (1610), posing as a third man between the two extreme positions for and against astrology, Kepler advocated that a definite relationship between heavenly phenomena and earthly events could be established.

At least 800 horoscopes and natal charts drawn up by Kepler are still extant, several of himself and his family, accompanied by some unflattering remarks. As part of his duties as district mathematician to Graz, Kepler issued a prognostication for 1595 in which he forecast a peasant uprising, Turkish invasion and bitter cold, all of which happened and brought him renown. Kepler is known to have compiled prognostications for 1595 to 1606, and from 1617 to 1624. As court mathematician, Kepler explained to Rudolf II the horoscopes of the Emperor Augustus and Muhammad, and Kepler gave astrological prognosis for the outcome of a war between the Republic of Venice and Paul V. In the On the new star (1606) Kepler explicated the meaning of the new star of 1604 as the conversion of America, downfall of Islam and return of Christ. The De cometis libelli tres (1619) is also replete with astrological predictions.

Kepler on God

"I was merely thinking God's thoughts after him. Since we astronomers are priests of the highest God in regard to the book of nature," wrote Kepler, "it benefits us to be thoughtful, not of the glory of our minds, but rather, above all else, of the glory of God."

Writings by Kepler

Mysterium Cosmographicum (The Sacred Mystery of the Cosmos) (1596)
Astronomiae Pars Optica (The Optical Part of Astronomy) (1604)
De Stella nova in pede Serpentarii (On the New Star in Ophiuchus's Foot) (1604)
Astronomia nova (New Astronomy) (1609)
Dioptrice (Dioptre) (1611)
Nova stereometria doliorum vinariorum (New Stereometry of wine barrels) (1615)
Epitome astronomiae Copernicanae (published in three parts from 1618–1621)
Harmonice Mundi (Harmony of the Worlds) (1619)
Tabulae Rudolphinae (1627)
Somnium (The Dream) (1634) - considered the first precursor of science fiction.

References

Peter Barker and Bernard R. Goldstein: "Theological Foundations of Kepler's Astronomy". Osiris, Volume 16: Science in Theistic Contexts. University of Chicago Press, 2001.
Max Caspar: Kepler; transl. and ed. by C. Doris Hellman; with a new introduction and references by Owen Gingerich; bibliographic citations by Owen Gingerich and Alain Segonds. New York: Dover, 1993 ISBN 0-486-67605-6
James A. Connor: Kepler's Witch: An Astronomer's Discovery of Cosmic Order Amid Religious War, Political Intrigue, and the Heresy Trial of His Mother. HarperSanFrancisco, 2004 ISBN 0-06-052255-0
J.V. Field: Kepler's geometrical cosmology. Chicago: Chicago University Press, 1988 ISBN 0-226-24823-2
Owen Gingerich: The eye of heaven: Ptolemy, Copernicus, Kepler. New York: American Institute of Physics, 1993 ISBN 0-88318-863-5 (Masters of modern physics; v. 7)
Kitty Ferguson: The nobleman and his housedog: Tycho Brahe and Johannes Kepler: the strange partnership that revolutionized science. London : Review, 2002 ISBN 0-747270-22-8 (published in the US as: Tycho & Kepler: the unlikely partnership that forever changed our understanding of the heavens. New York: Walker, 2002 ISBN 0-8027-1390-4)
Arthur Koestler: The Sleepwalkers: A History of Man's Changing Vision of the Universe. (1959). ISBN 0-140-19246-8
John Lear: Kepler's Dream. Berkeley: University of California Press, 1965.
Bruce Stephenson: Kepler's physical astronomy. New York: Springer, 1987 ISBN 0-387-96541-6 (Studies in the history of mathematics and physical sciences; 13)

Kepler in fiction

John Banville: Kepler: a novel. London: Secker & Warburg, 1981 ISBN 0-436-03264-3 (and later eds.). Also published: Boston, MA:Godine, 1983 ISBN 0-87923-438-5. Draws heavily on Koestler's account of Kepler in The Sleepwalkers.

Named in Kepler's honor

Kepler Space Observatory, a solar-orbiting, planet-hunting telescope due to be launched by NASA in 2008.
The Kepler Solids, a set of geometrical constructions, two of which were described by him.
Kepler's Star, Supernova 1604, which he observed and described.
Kepler conjecture about sphere packing, proved true 400 years later.
Kepler, a crater on the moon
Kepler, a crater on Mars
1134 Kepler is an asteroid.
In 1975, nine years after its founding, the College for Social and Economic Sciences Linz (Austria) was renamed Johannes Kepler University Linz in honor of Johannes Kepler, since he wrote his magnum opus Harmonice Mundi in Linz.
Johannes Kepler's Gymnasium in Prague
Keplerstraße in Hanau near Frankfurt am Main