|
|
Das Pentagramm, Pentagon und irrationale Zahlen
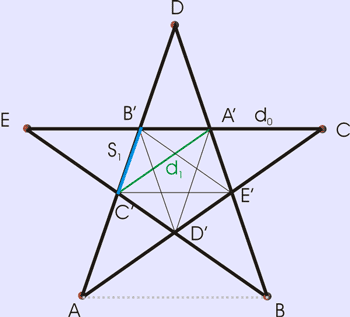
AB = BA', BE' = A'D EB/BA' = BA'/DB' = DB'/B'C' = 1.618033989.... (golden ratio) The Pythagoreans used the Pentagon star (Pentagram) formed by the five diagonals of a regular Pentagon as a symbol of their school. It was probably this reason that they studied its geometrical properties and that they discovered that this symbol contradicts their idea that everything can be expressed by integer numbers or ratio of integer numbers. Pentagram is a greek word for “pente grammes”, i.e. five lines. Sometimes it is called also a pentalpha, as it looks consisting of 5 rotated “A” symbols.
Agrippa von Nettesheim (Heinrich Cornelius ) (1486 – 1535) , De occulta philosophia point on the line". I have no direct information of a text by the ancient Greeks which discusses the Fibonacci numbers but I found the following information interesting ( Source ) : Epidaurus Theater: The place for the spectators was divided into two tiers: the first one had 34 rows of places, the second one 21. The angle between theatron and scene divides a circumference of the basis of an amphitheater in ratio: 137°,5 : 222°,5 = 0.618. Dionysus Theater Athens: Three tiers. The first tier has 13 sectors, the second one 21 sectors. Now 13, 21 and 34 are Fibonacci numbers (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...) with the property that the ratio an+1/an converges to phi. LINKS Thrace, Cherronesos, circa 400-350 BC, AR Hemidrachm. Lion / Pentagram and VE monogram Triangular, Quadratic and Pentagonal Numbers Visual Explanations and the Pentagon (PDF File) The Pythagorean Pentacle (Strange Theories)and more strange stories: Coins with Pentagrams and the fact that the Pentagram of the Greeks is always with the two vertices on the top! Inscribing a regular pentagon in a circle – and proving it Phillip S. Jones, Irrationals or Incommensurables. I. Their discovery, and a "Logical Scandal". Mathematics Teacher 49, 123-27 (1956)
 |
|
|||||||||||||||||